Backpropagation for Linear Regression1

Linear Regression을 위한 Backpropagation은 다음과 같은 모델들을 사용하여 순서대로 진행될 것이다.

1. $y = \theta x$
2. $y = \theta_{1} x + \theta_{0}$
3. $y = \theta_{2} x_{2} + \theta_{1} x_{1} + \theta_{0}$

그리고 각 단계에서도 첫 번째로는 하나의 sample에 대한 backpropagation, 두 번째로는 2개의 sample에 대한 backpropagation, 마지막으로 Vectorized form의 backpropagation으로 진행될 것이다.

 

그러면 이번 포스트에서는 첫 번째 model부터 살펴보도록하자.

 

Backpropagation for One Sample

---

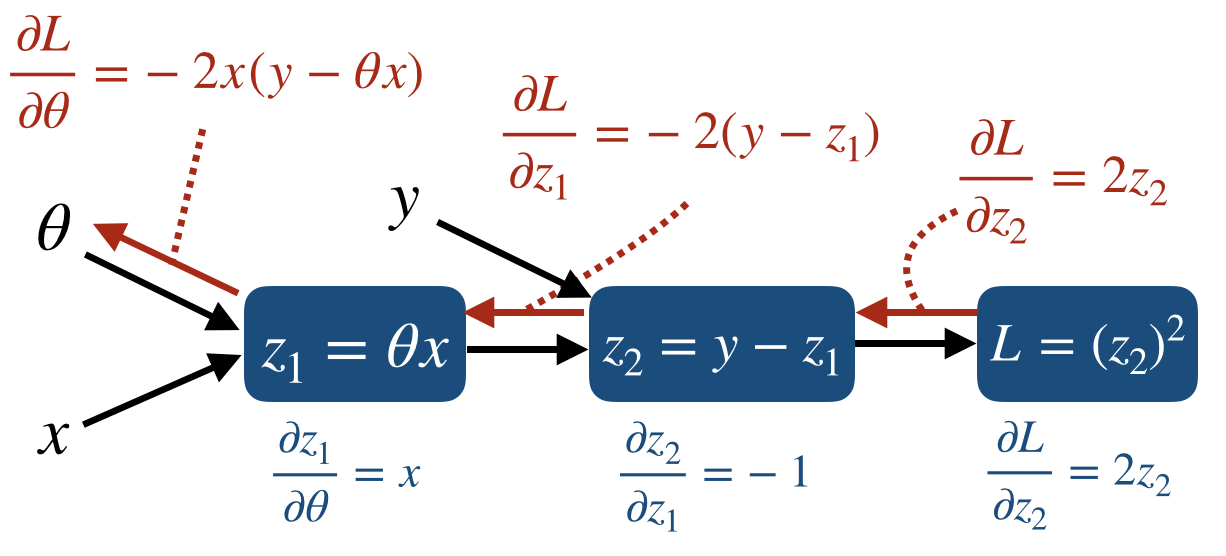
먼저 forward-backward propagation을 위한 node들을 먼저 만들어보면 다음과 같다.

 

 

즉, $z_{1}$ node는 prediction value가 될 것이고, $L$는 loss를 구하게 된다. 그리고 각 node에서의 partial derivative를 구하면 다음과 같이 표시할 수 있다.

 

 

그리고 Chain rule에 의해 $\theta$까지의 backpropagation을 계산하면 다음과 같다.

 

$\frac{\partial L}{\partial z_{1}} = 

\frac{\partial L}{\partial z_{2}} \frac{\partial z_{2}}{\partial z_{1}}

=
2z_{2}*(-1) = -2z_{2}

=-2(y-z_{1})$

 

$\frac{\partial L}{\partial \theta} = 

\frac{\partial L}{\partial z_{2}}
\frac{\partial z_{2}}{\partial z_{1}}
\frac{\partial z_{1}}{\partial \theta}

=

\frac{\partial L}{\partial z_{1}}
\frac{\partial z_{1}}{\partial \theta}

=-2x(y-z_{1})
=-2x(y-\theta x)$

 

따라서 Backpropagation은 다음과 같이 일어난다.

 

$\theta = \theta - lr * \frac{\partial L}{\partial \theta}
=
\theta - lr * (-2x(y- \theta x))
=
\theta + lr * 2x(y- \theta x)$

 

Backpropagation for Two Samples

---

 

우리가 Learning 단계에서 mini-batch를 사용한다면 loss가 아닌 cost를 parameter update에 사용하게 된다. 

 

즉, loss들의 평균을 구하는 node가 추가된다. 그리고 mini-batch size가 2인 linear regression model은 다음과 같다.

 

그리고 각 node에서의 partial derivative를 표시하면

이 되고, Chain rule을 이용하여 backpropagation을 계산하면 다음과 같다.

 

$\frac{\partial J}{\partial z_{2}^{(1)}}=\frac{\partial J}{\partial L^{(1)}}\frac{\partial L^{(1)}}{\partial z_{2}^{(1)}}=\frac{1}{2} * 2z_{2}^{(1)}$

 

$\frac{\partial J}{\partial z_{2}^{(2)}}=\frac{\partial J}{\partial L^{(2)}}\frac{\partial L^{(2)}}{\partial z_{2}^{(2)}}=\frac{1}{2} * 2z_{2}^{(2)}$

 

$\frac{\partial J}{\partial z_{1}^{(1)}}=\frac{\partial J}{\partial L^{(1)}}\frac{\partial L^{(1)}}{\partial z_{2}^{(1)}}\frac{\partial z_{2}^{(1)}}{\partial z_{1}^{(1)}}=\frac{\partial J}{\partial z_{2}^{(1)}}\frac{\partial z_{2}^{(1)}}{\partial z_{1}^{(1)}}=-\frac{1}{2} * 2z_{2}^{(1)}=-\frac{1}{2} *2(y^{(1)} - z_{1}^{(1)})$

 

$\frac{\partial J}{\partial z_{1}^{(2)}}=\frac{\partial J}{\partial L^{(2)}}\frac{\partial L^{(2)}}{\partial z_{2}^{(2)}}\frac{\partial z_{2}^{(2)}}{\partial z_{1}^{(2)}}=\frac{\partial J}{\partial z_{2}^{(2)}}\frac{\partial z_{2}^{(2)}}{\partial z_{1}^{(2)}}=-\frac{1}{2} * 2z_{2}^{(2)}=-\frac{1}{2} *2(y^{(2)} - z_{1}^{(2)})$

 

$\frac{\partial J}{\partial \theta}=\frac{\partial J}{\partial L^{(1)}}\frac{\partial L^{(1)}}{\partial z_{2}^{(1)}}\frac{\partial z_{2}^{(1)}}{\partial z_{1}^{(1)}}\frac{\partial z_{1}^{(1)}}{\partial \theta}=\frac{\partial J}{\partial z_{1}^{(1)}}\frac{\partial z_{1}^{(1)}}{\partial \theta}=-\frac{1}{2} *2x^{(1)}(y^{(1)} - z_{1}^{(1)})=-\frac{1}{2} *2x^{(1)}(y^{(1)} - \theta x^{(1)})$

 

$\frac{\partial J}{\partial \theta}=\frac{\partial J}{\partial L^{(2)}}\frac{\partial L^{(2)}}{\partial z_{2}^{(2)}}\frac{\partial z_{2}^{(2)}}{\partial z_{1}^{(2)}}\frac{\partial z_{1}^{(2)}}{\partial \theta}=\frac{\partial J}{\partial z_{1}^{(2)}}\frac{\partial z_{1}^{(2)}}{\partial \theta}=-\frac{1}{2} *2x^{(2)}(y^{(2)} - z_{1}^{(2)})=-\frac{1}{2} *2x^{(2)}(y^{(2)} - \theta x^{(2)})$

 

이를 visualization하면 다음과 같다.

 

따라서 parameter update는 다음과 같이 된다.

 

$\theta = \theta - lr * (-\frac{1}{2} *2x^{(1)}(y^{(1)} - \theta x^{(1)}) -\frac{1}{2} *2x^{(2)}(y^{(2)} - \theta x^{(2)}))=\theta + lr * \frac{1}{2} \sum_{i=1}^{2} 2x^{(i)}(y^{(i)} - \theta x^{(i)})$

 

 

Backpropagation Vectorized form

---

위의 두 번째 단계는 실제 프로그래밍을 하기에도 힘들고, 같은 연산이 반복될 때 사용되는 vectorization을 이용하지 못한 모양이다. 따라서 mini-batch 사이즈가 임의의 n개일 때는 vectorization form을 이용하게 되고, 이 포스트에서는 3개의 mini-batch에 대한 backpropagation을 다룬다.

 

먼저 forward propgation을 포함한 model은 다음과 같다.

 

 

그리고 각 node에서 Jacobian을 이용한 partial derivative를 표시하면 다음과 같다.

 

 

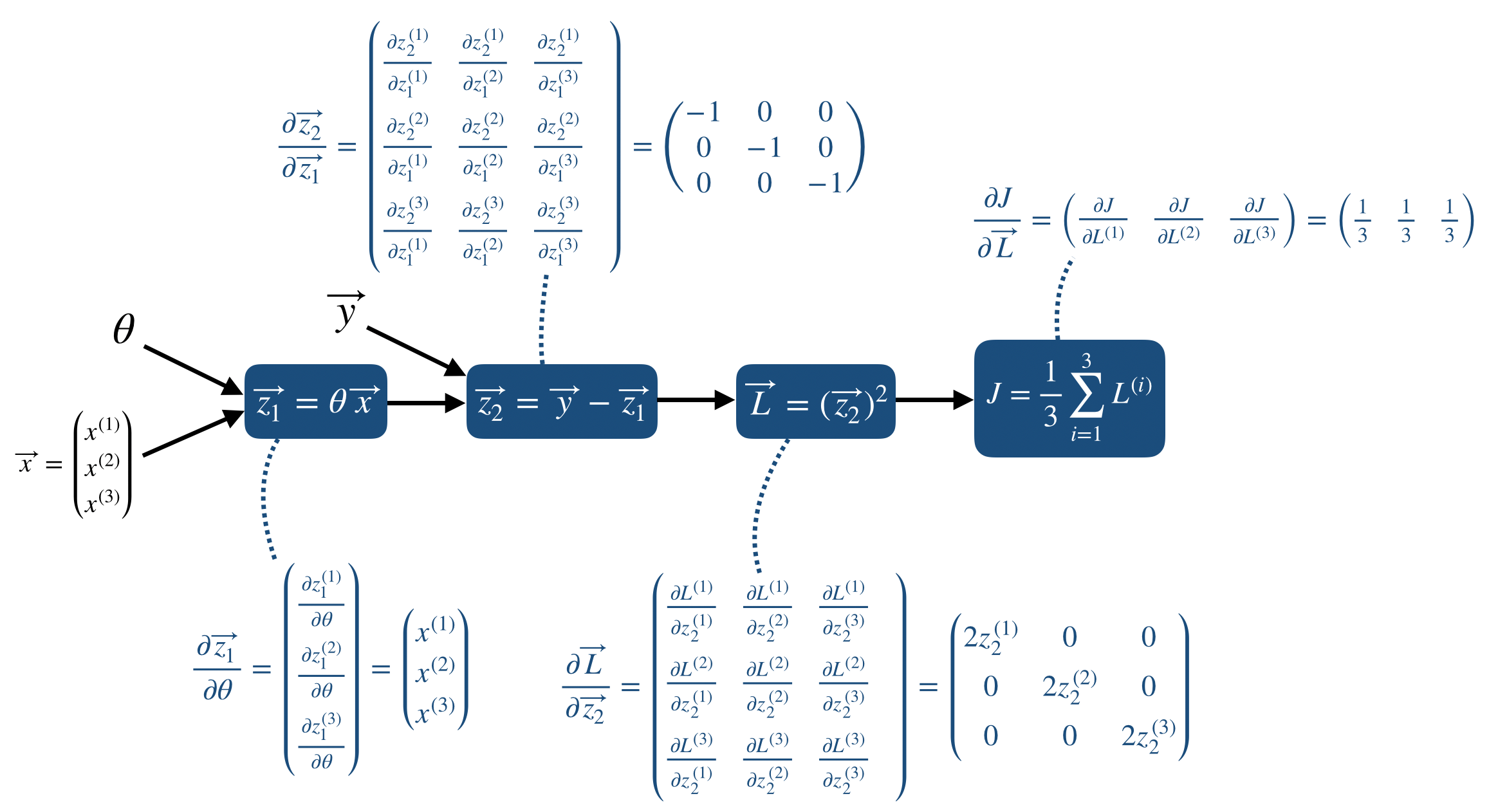
그리고 각 node에서 실제로 backpropagationdmf 계산하면 다음과 같다.

따라서 Backpropagation은 다음과 같이 전체적으로 표시할 수 있다.