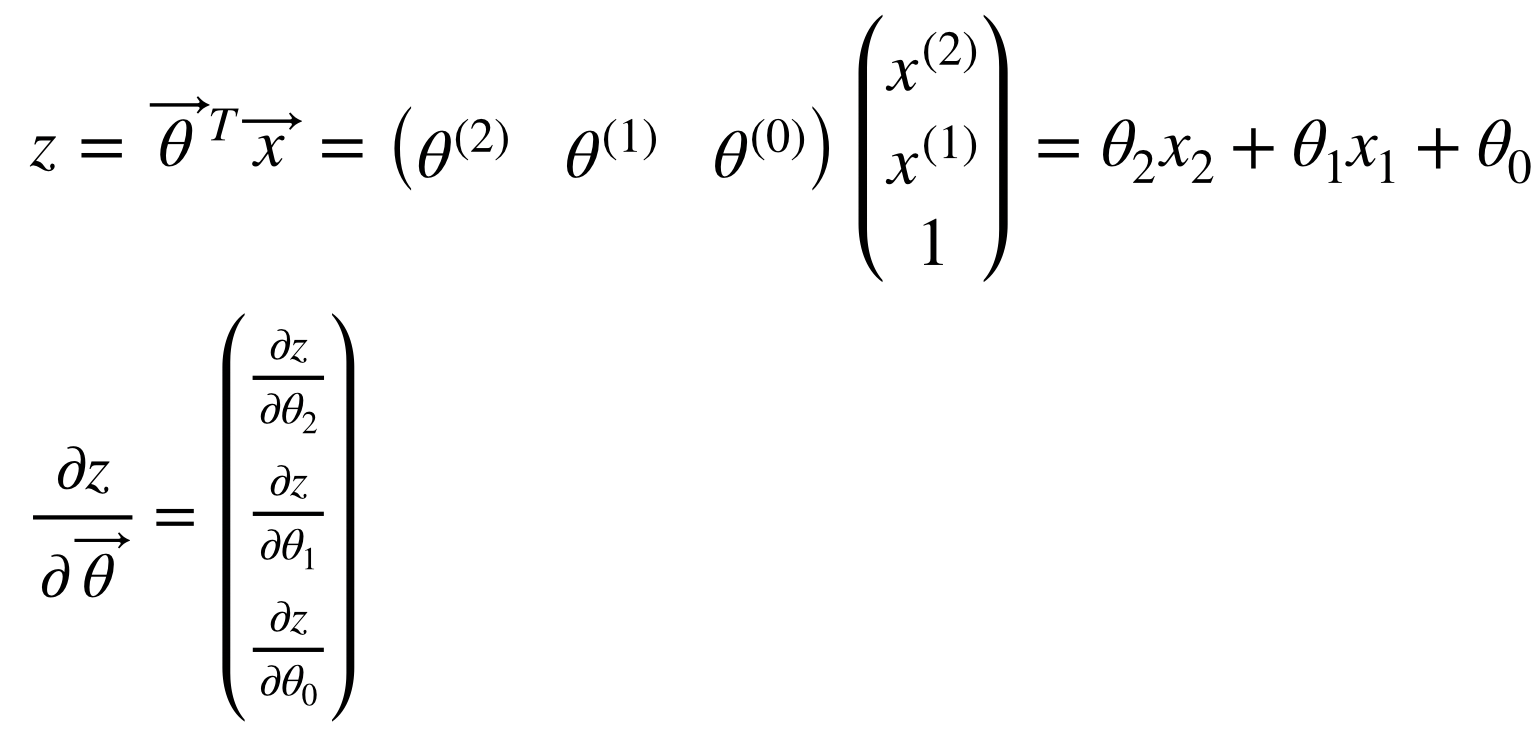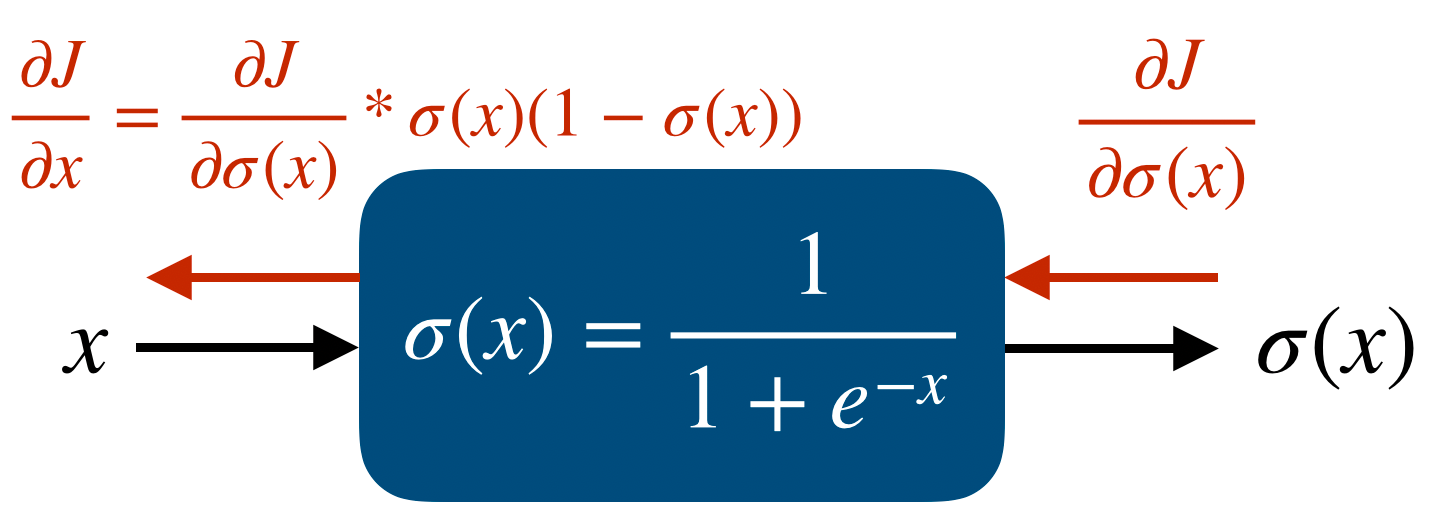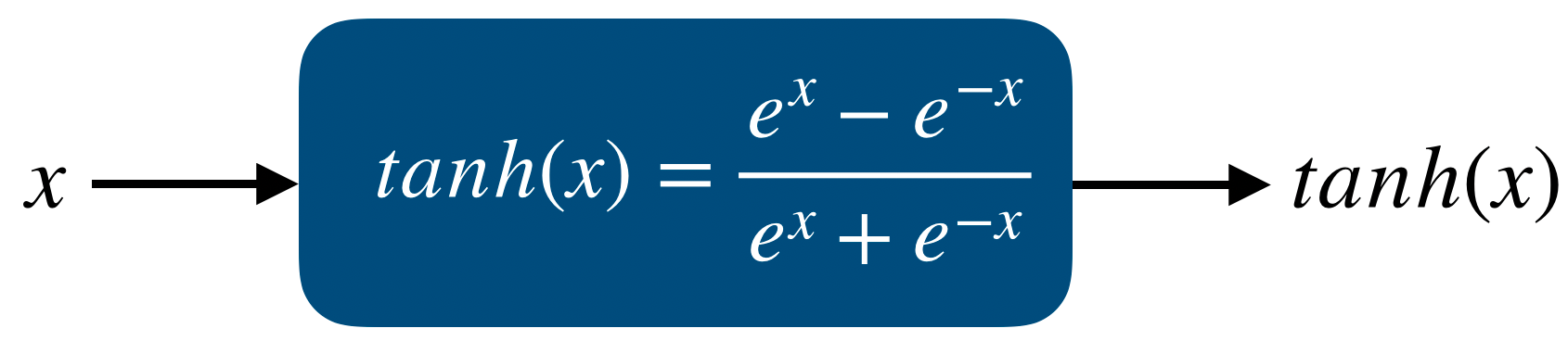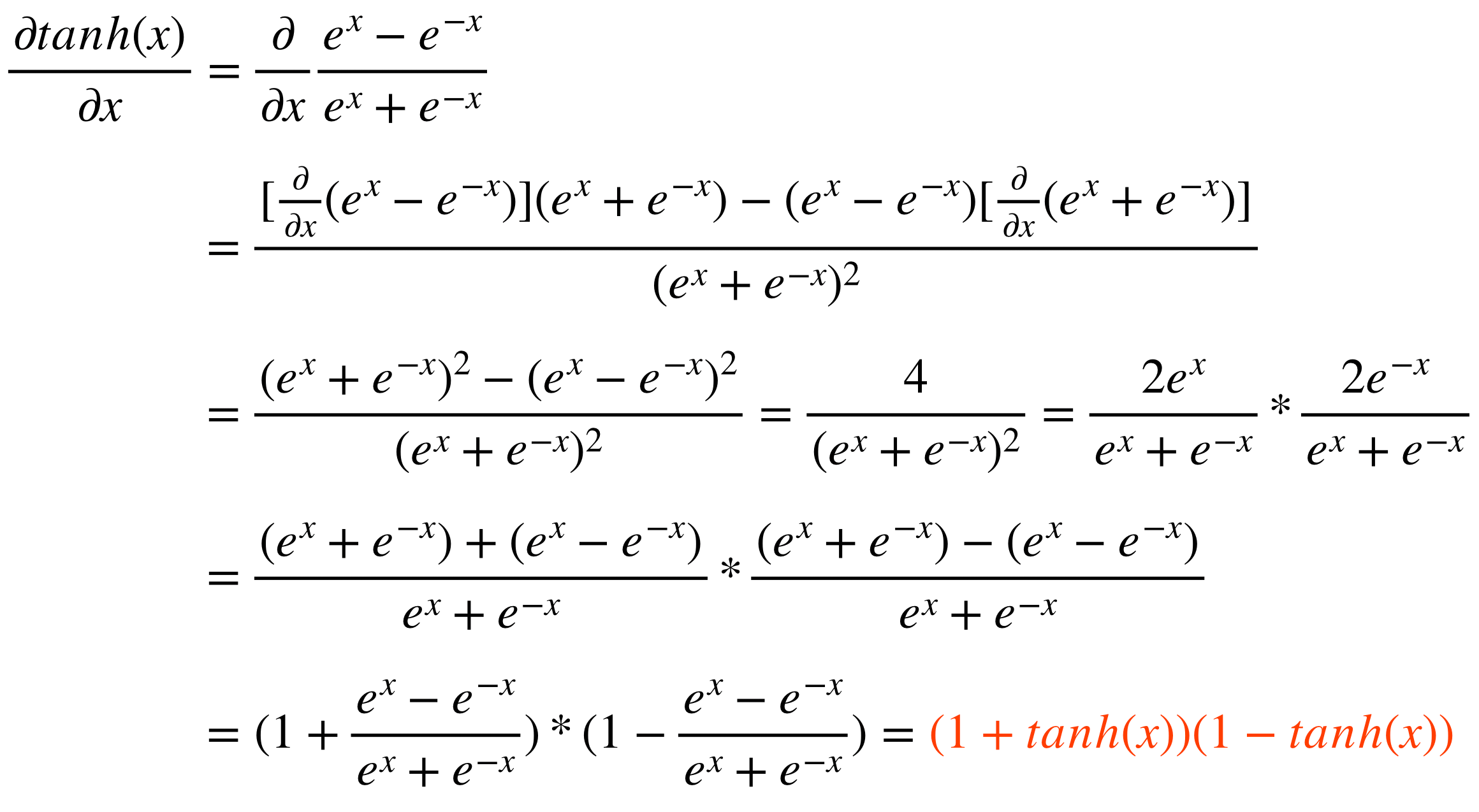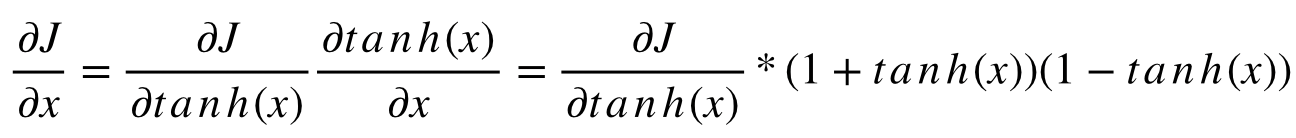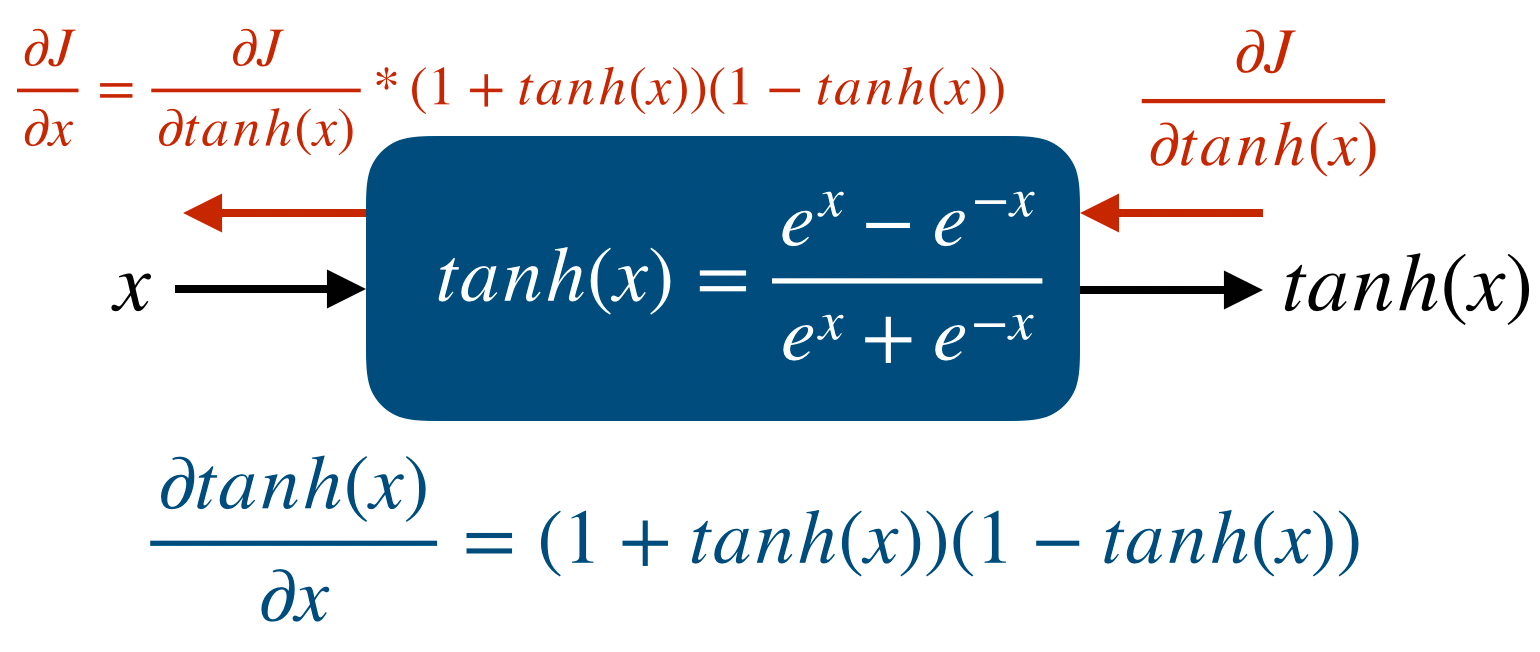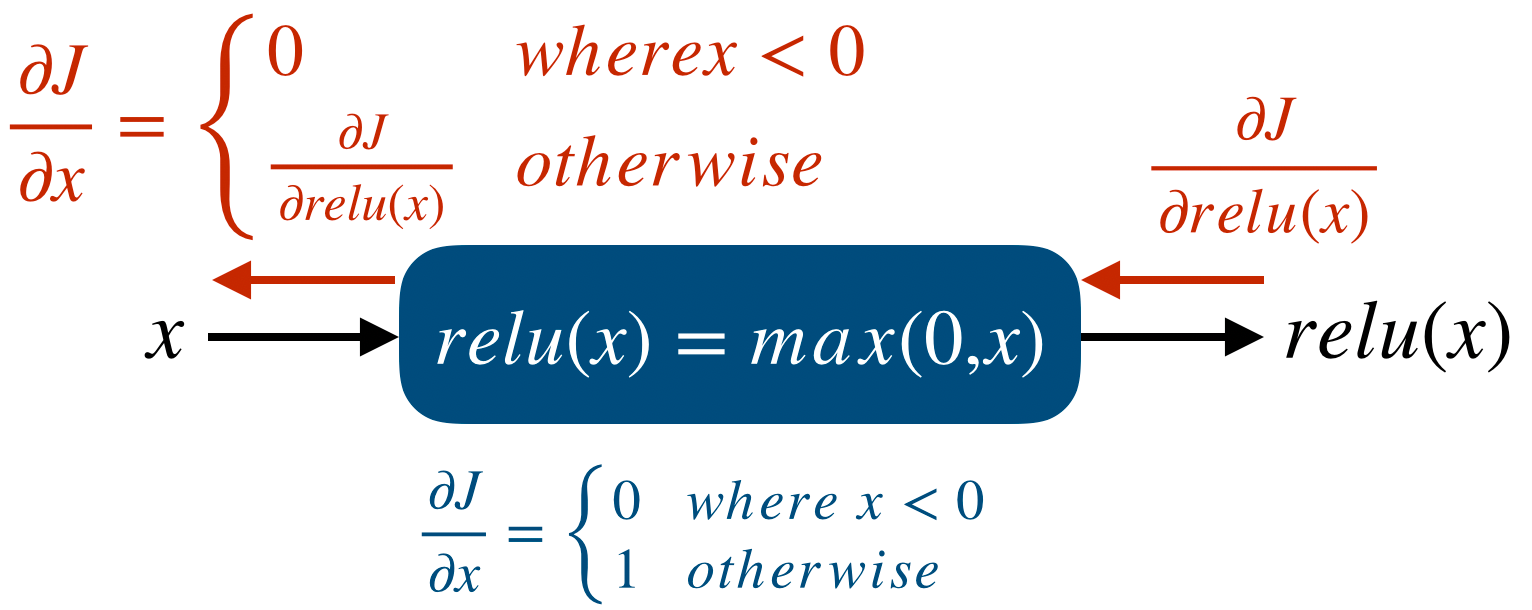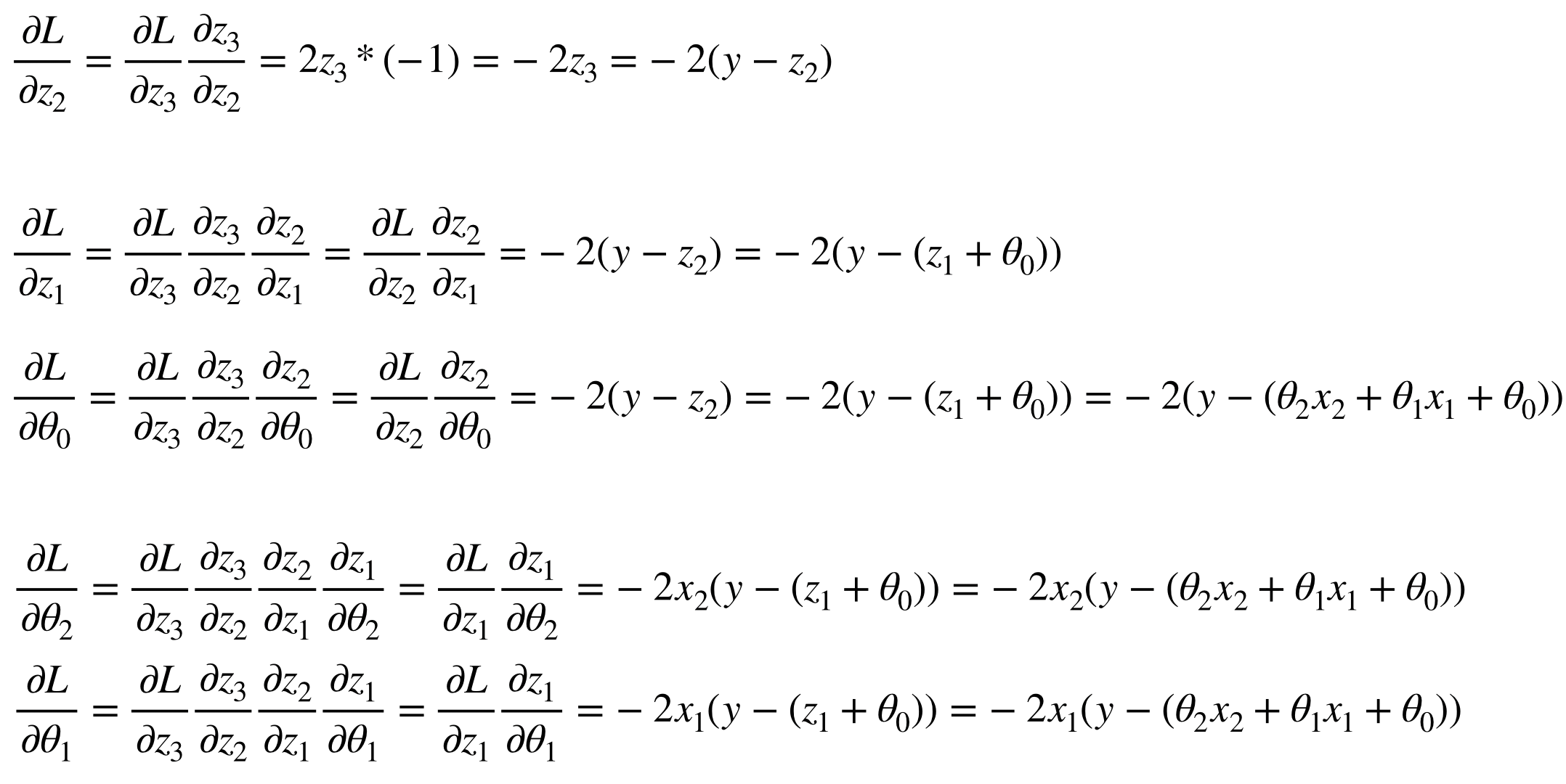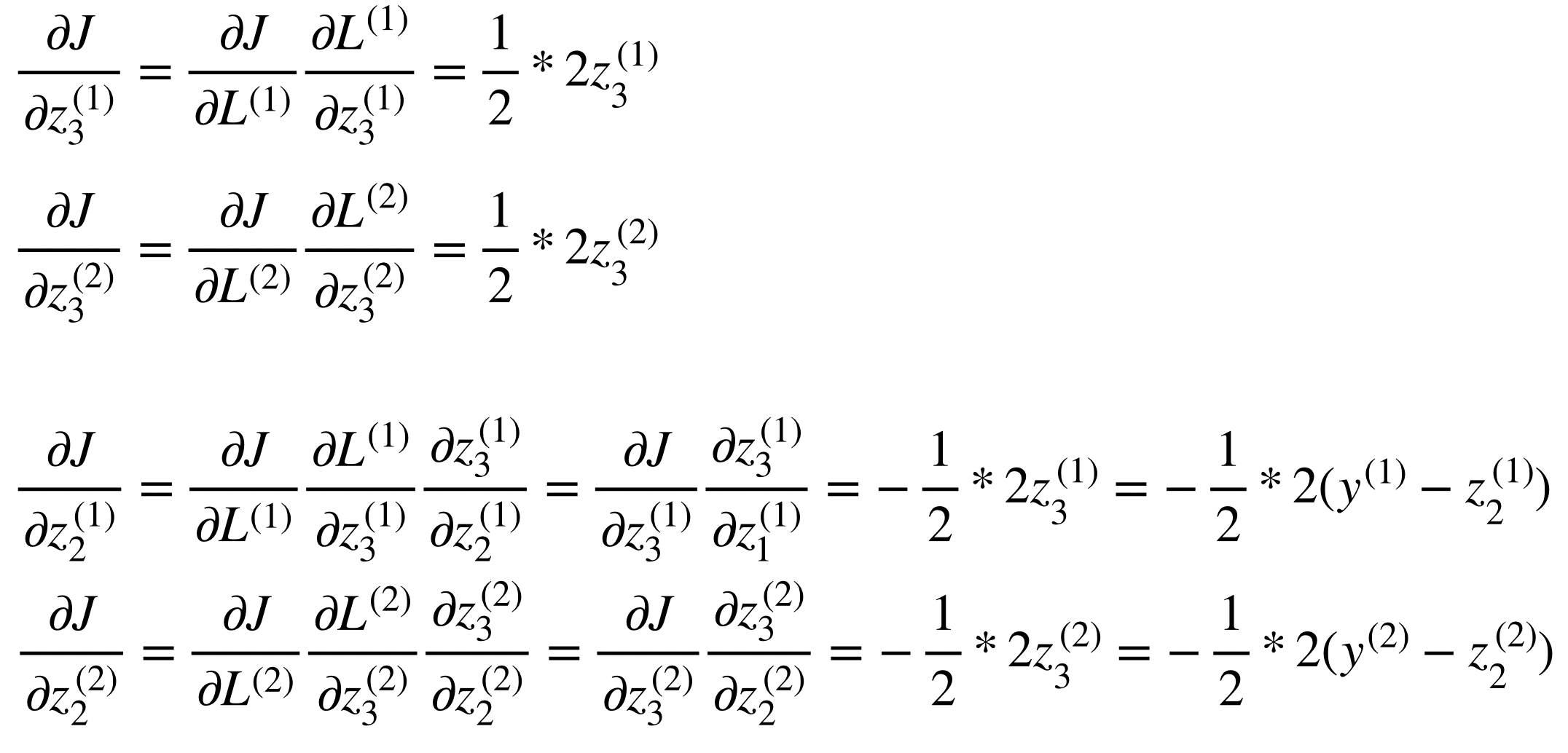tf.GradientTape
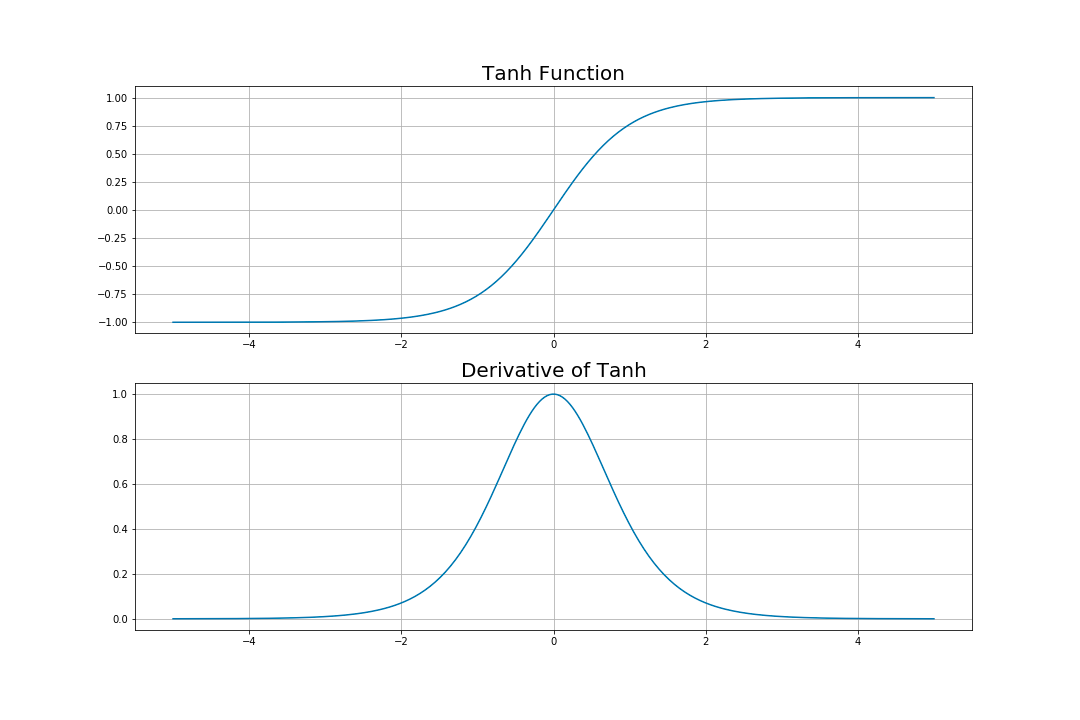
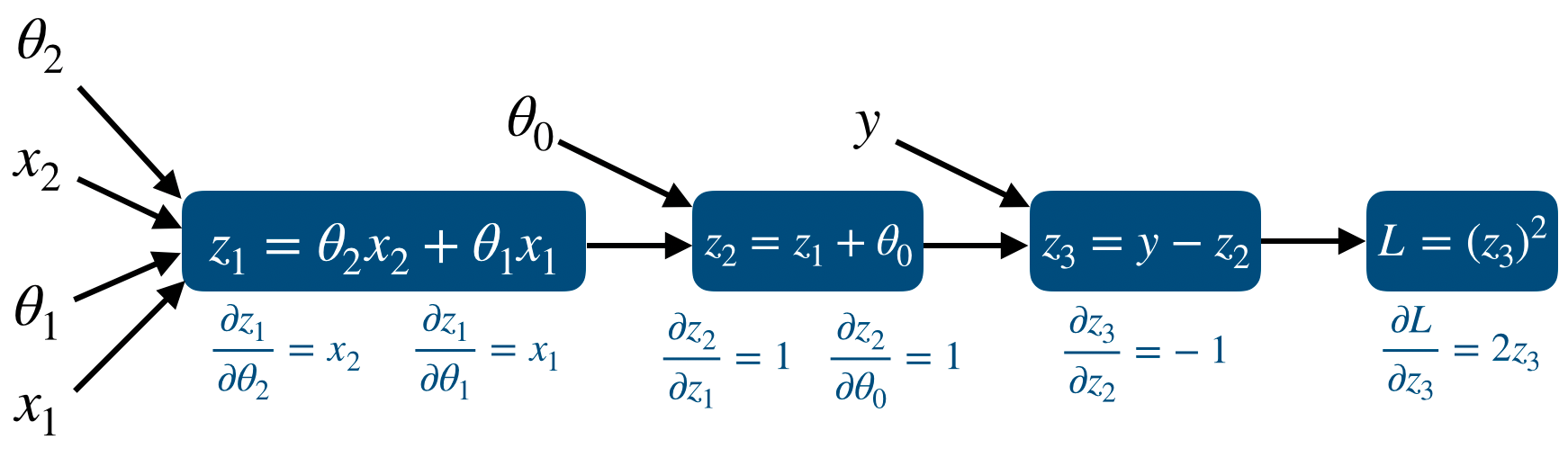
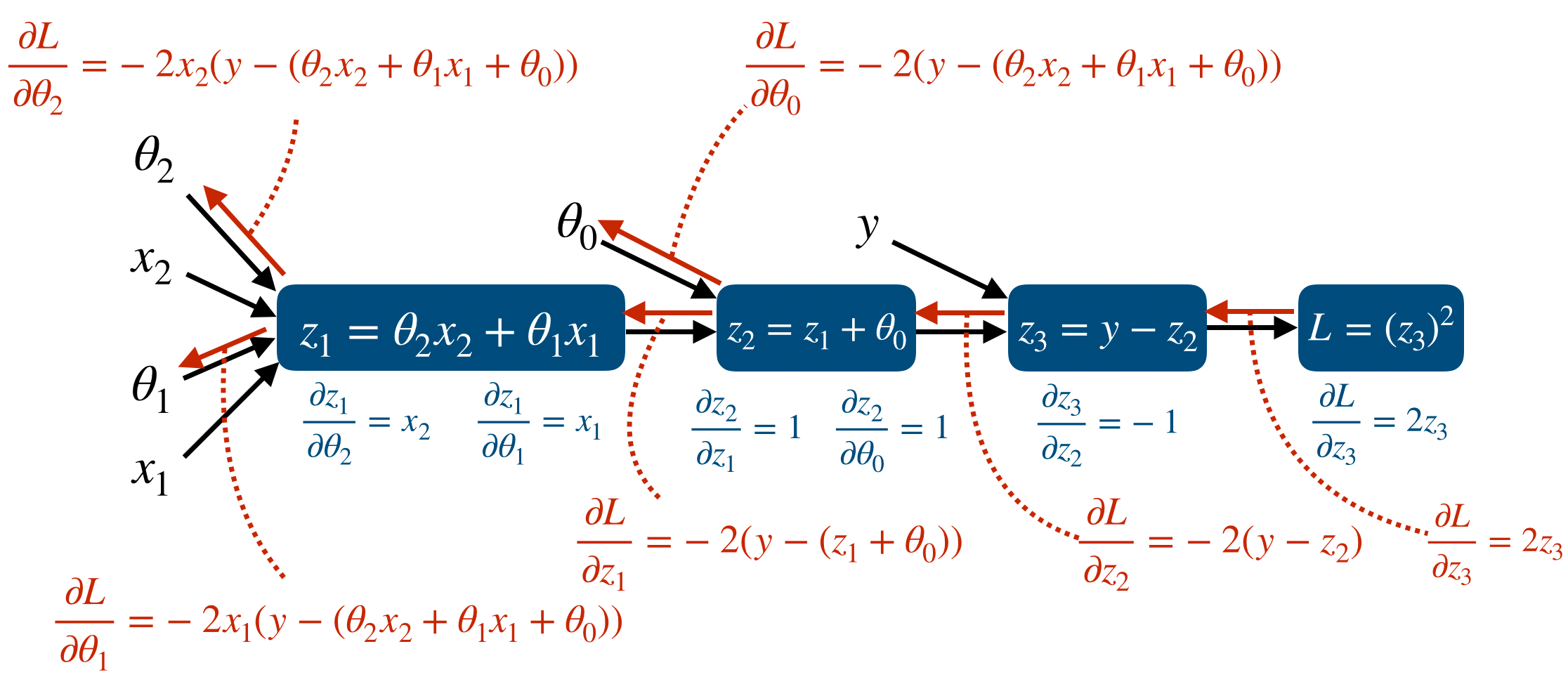
Neural network를 만든다는 것은 곧 computational graph를 만든다는 것이다. 즉 node와 edge를 만들어 network computation을 만든다. 일반적인 computational graph와는 다르게 deep learning에서는 prediction과 loss를 연산하는 forward propagation과 partial derivative와 vector chain rule을 이용한 backpropagation이 존재한다.
우리가 Tensorflow와 같은 deep learning framework를 이용하는 가장 큰 이유는 이 forward/backward propagation을 쉽게 구현할 수 있도록 도와주는 Automatic Differentiation 기능일 것이다. 이는 forward propagation에서 일어나는 모든 연산에 대해 gradient를 자동으로 저장해주고 이를 통해 gradient descent method를 쉽게 사용할 수 있게 해준다.
그리고 backpropagation을 연산할 때 하나하나 gradient를 구하는 것이 아니라 forward propagation이 진행될 때 이 값들을 저장해두면 backpropagation에서 이 저장된 값들을 이용하여 훨씬 빠르게 연산이 가능하다. 이때 tf.GradientTape에는 forward propagation이 진행되면서 나중에 backpropagation을 할 때 필요한 값들을 저장해둔다.
정리하면 이렇다. backpropagation을 할 때 forward propagation 값들을 저장해두면 이를 이용해 훨씬 빠르게 연산을 할 수 있다. 따라서 forward propagation이 진행되는 동안 그 값들을 저장할 필요가 있다. 즉, prediction을 구하는 과정과 loss를 구하는 과정이 tf.GradientTape의 대상이 되는 것이다.
tf.GradientTape Exmaple
이 gradient tape을 설명하는데 글로만 주구장창 말하는 것보다 예를 드는 것이 더 이해하기 쉬울 것 같아 예시를 들어보려고 한다.
test_list1 = [1, 2, 3]
test_list2 = [10, 20, 30]
t1 = tf.Variable(test_list1, dtype=tf.float32)
t2 = tf.Variable(test_list2, dtype=tf.float32)
with tf.GradientTape() as tape:
t3 = t1 * t2
gradients = tape.gradient(t3, [t1, t2])
print(gradients[0])
'''
tf.Tensor([10. 20. 30.], shape=(3,), dtype=float32)
'''
print(gradients[1])
'''
tf.Tensor([1. 2. 3.], shape=(3,), dtype=float32)
'''위에서는 variable tensor 2개를 만들고 gradient tape에서 이를 곱하는 t3를 만들었다. 그러면 Tensorflow는 t1, t2 node를 이용해 t3를 구하는 computational graph를 만든다. 그리고 이에 대한 연산값들을 저장한다.
그 뒤에 gradient를 구하는 과정은 tape.gradient이다. 첫 번째 t3는 target이므로 보통 loss가 된다. 그리고 그 뒤에는 우리가 학습시키려는 variable tensor를 넣어주면 된다. 이때 gradients[0]은 t3에 대한 t1의 gradient, gradients[1]는 t3에 대한 t2의 gradient가 된다.
위의 결과에서 알 수 있듯이, t3를 구하는데 t1과 t2를 element-wise로 곱했으므로 그 결과는 서로의 vector가 된다. 그 결과로 각자 이론과 동일한 결과를 얻을 수 있다.
앞선 포스팅에서 Tensorflow에서 기본적인 tensor는 두 가지가 있다고 했고 이는 constant tensor와 variable tensor이다. 그리고 이들은 각각 input/label, trainable variable이 된다고 했다. 따라서 우리는 constant tensor에 대한 gradient를 구하는 것은 시간 낭비가 될 것이다. 다음 예제를 살펴보자.
test_list1 = [1, 2, 3]
test_list2 = [10, 20, 30]
t1 = tf.constant(test_list1, dtype=tf.float32)
t2 = tf.Variable(test_list2, dtype=tf.float32)
with tf.GradientTape() as tape:
t3 = t1 * t2
gradients = tape.gradient(t3, [t1, t2])
print(gradients[0])
'''
None
'''
print(gradients[1])
'''
tf.Tensor([1. 2. 3.], shape=(3,), dtype=float32)
'''위의 결과에서 t3에 대한 t1의 gradient는 구해지지 않았고 t2의 gradient는 구해졌다. 이처럼 Tensorflow는 학습이 필요없는 node에 대해서는 gradient가 구해지지 않음을 알 수 있다.
Simple Linear Regression Example
simple linear regression은 predictor가 y=wx + b인 regression이다. 따라서 weight, bias는 모두 1개이고 loss는 mean squared error를 사용한다. 이를 위한 toy dataset은 다음과 같이 tf.constant로 만들어줄 수 있다.
x_data = tf.constant([-1, -0.5, 0.5, 1], dtype=tf.float32)
y_data = 3*x_data + 1
학습을 위한 trainable parameter인 w, b는 다음과 같이 tf.Variable로 만들어준다
w = tf.Variable(-1.)
b = tf.Variable(-1.)그리고 learning rate은 0.1로, w와 b의 변화를 추적하기 위한 w_trace, b_trace를 만들어준다.
LR = 0.1
w_trace, b_trace = [], []
그 후에 학습이 진행되는 코드는 다음과 같다.
for epoch in range(10):
for x, y in zip(x_data, y_data):
with tf.GradientTape() as tape:
predictions = w*x + b
loss = (predictions - y)**2
gradients = tape.gradient(loss, [w, b])
w = tf.Variable(w - LR*gradients[0])
b = tf.Variable(b - LR*gradients[1])
w_trace.append(w.numpy())
b_trace.append(b.numpy())위에서 알 수 있듯이 prediction과 loss를 계산하는 부분은 tf.GradientTape 안에 있다. 이때 backpropagation을 위한 값들이 저장되고, gradient는 w, b에 대해 구한다. 마지막으로 SGD를 이용하여 w, b를 update하면 된다. 그리고 w, b의 update되는 상태는 다음과 같다.
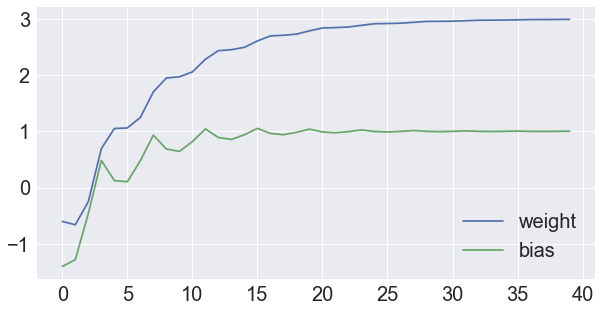
이처럼 tf.GradientTape은 forward propagation에 필요하다는 개념만 알면 이후에 오는 학습 코드들도 어렵지 않게 받아들일 수 있을 것이다.
'TensorFlow2 A to Z' 카테고리의 다른 글
| [Tensorflow2 강의자료] 3. Tensor Operations (0) | 2020.09.29 |
|---|---|
| [Tensorflow2 강의자료] 2. Making Tensors2 (0) | 2020.09.28 |
| [Tensorflow2 강의자료] 1. Making Tensors (0) | 2020.09.28 |